I was familiar with Python as an introduction language fro programming, I tried a couple of time a long time ago. The main impression that I had was that it is a bit slow although it still quite reasonable choice for prototyping specially it is free and platform independent.
I thought to revisit my old interest in Python, and here is an implementation of Julia sets that I fetched from a lecture on YouTube, one of many available that was delivered at scipy conferences. The problem is that I connot remember which one now that I watched.
import numpy as np
from time import time
def kernel(z, c, lim, cutoff=1e6):
''' Computes the number, `n`, of iterations necessary such that
|z_n| > `lim`, where `z_n = z_{n-1}**2 + c`.
'''
count = 0
while abs(z) < lim and count < cutoff:
z = z * z + c
count += 1
return count
def compute_julia(c, N, bound=2, lim=1000., kernel=kernel):
''' Pure Python calculation of the Julia set for a given `c`.
No NumPy array operations are used.
'''
julia = np.empty((N, N), dtype=np.uint32)
grid_x = np.linspace(-bound, bound, N)
grid_y = grid_x * 1j
c = complex(c)
t0 = time()
for i, x in enumerate(grid_x):
for j, y in enumerate(grid_y):
julia[i,j] = kernel(x+y, c, lim)
return julia, time() - t0
The plotting part are as given below
import pylab as pl
def plot_julia(kwargs, compute_julia):
''' Given parameters dict in `kwargs` and a function to compute the Julia set (`compute_julia`), plots the
resulting Julia set with appropriately labeled axes.
'''
kwargs = kwargs.copy()
def _plotter(kwargs):
bound = kwargs['bound']
julia, time = compute_julia(**kwargs)
print "execution time (s):", time
julia = np.log(julia)
pl.imshow(julia,
interpolation='nearest',
extent=(-bound, bound)*2)
pl.colorbar()
title = r"Julia set for $C={0.real:5.3f}+{0.imag:5.3f}i$ $[{1}\times{1}]$"
pl.title(title.format(kwargs['c'], kwargs['N']))
pl.xlabel("$Re(z)$")
pl.ylabel("$Im(z)$")
pl.figure(figsize=(14, 12))
cvals = [0.285+0.01j, -0.1+0.651j, -0.4+0.6j, -0.8+0.156j]
subplots = ['221', '222', '223', '224' ]
for c, sp in zip(cvals, subplots):
kwargs.update(c=c)
pl.subplot(sp)
_plotter(kwargs)
pl.show()
kwargs = dict(N=1000, bound=1.5)
plot_julia(kwargs, compute_julia)
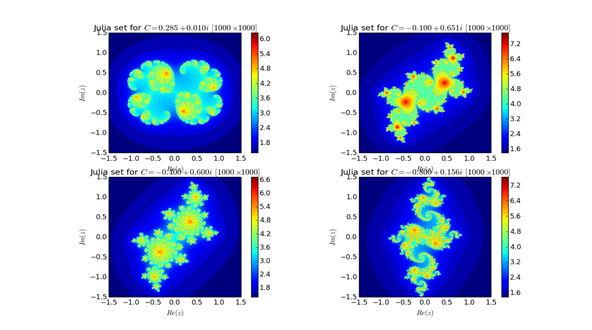
The execution times for the four figures was
execution time (s): 37.7200000286 execution time (s): 97.0900001526 execution time (s): 44.8949999809 execution time (s): 72.1289999485
Somewhat slow !!
The matlab implementation of the same function are shorter and considerably faster.
function julia = compute_julia(N, bound, c)
julia = uint32(zeros(N, N));
grid_x = linspace(-bound, bound, N);
grid_y = grid_x * 1j;
for j = 1:N
for i = 1:N
julia(i,j) = kernel(grid_x(i)+grid_y(j), c);
end
end
end
function count = kernel(z, c)
%Computes the number, `n`, of iterations necessary such that
%|z_n| > `lim`, where `z_n = z_{n-1}**2 + c`.
lim=1000;
count = 0;
cutoff=1e6;
while abs(z) < lim && count < cutoff
z = z * z + c;
count = count + 1;
end
end
julia = uint32(zeros(N, N));
grid_x = linspace(-bound, bound, N);
grid_y = grid_x * 1j;
for j = 1:N
for i = 1:N
julia(i,j) = kernel(grid_x(i)+grid_y(j), c);
end
end
end
function count = kernel(z, c)
%Computes the number, `n`, of iterations necessary such that
%|z_n| > `lim`, where `z_n = z_{n-1}**2 + c`.
lim=1000;
count = 0;
cutoff=1e6;
while abs(z) < lim && count < cutoff
z = z * z + c;
count = count + 1;
end
end
cvals = [0.285+0.01j, -0.1+0.651j, -0.4+0.6j, -0.8+0.156j];
for i = 1:4
tic; julia = compute_julia(1000, 1.5, cvals(i)); toc
subplot(2,2,i)
image(julia)
end
and here are the execution times
Elapsed time is 7.515207 seconds.
Elapsed time is 20.076634 seconds.
Elapsed time is 8.709530 seconds.
Elapsed time is 14.150072 seconds.
So, clearly the matlab is faster. But what if we used Cython with python and mex files with matlab? The cython implementation is really one of the best automatic code generation tools ever. The ease with which the conversion is done is unsurpassed.
First and since I am using the Ipython –notebook we have to load the Cython magic
%load_ext cythonmagic
%%cython
from time import time
import numpy as np
cimport cython
cimport numpy as cnp
ctypedef double complex cpx_t
ctypedef double real_t
cdef inline real_t cabs_sq(cpx_t z) nogil:
''' Helper inline function, computes the square of the abs.
value of the complex number `z`.
'''
return z.real * z.real + z.imag * z.imag
cpdef unsigned int kernel(cpx_t z,
cpx_t c,
real_t lim,
real_t cutoff=1e6) nogil:
''' Cython implementation of the kernel computation.
This is implemented so that no
C-API calls are made inside the function
body. Even still, there is some overhead as compared
with a pure C implementation.
'''
cdef unsigned int count = 0
cdef real_t lim_sq = lim * lim
while cabs_sq(z) < lim_sq and count < cutoff:
z = z * z + c
count += 1
return count
@cython.boundscheck(False)
@cython.wraparound(False)
def compute_julia_opt(cpx_t c,
unsigned int N,
real_t bound=1.5,
real_t lim=1000.):
'''
Cython `compute_julia()` implementation with Numpy array buffer
declarations and appropriate compiler directives. The body of this
function is nearly identical to the `compute_julia_no_opt()`
function.
'''
cdef cnp.ndarray[cnp.uint32_t, ndim=2, mode='c'] julia
cdef cnp.ndarray[real_t, ndim=1, mode='c'] grid
cdef unsigned int i, j
cdef real_t x, y
julia = np.empty((N, N), dtype=np.uint32)
grid = np.linspace(-bound, bound, N)
t0 = time()
for i in range(N):
x = grid[i]
for j in range(N):
y = grid[j]
julia[i,j] = kernel(x+y*1j, c, lim)
return julia, time() - t0
This only an alternative implementation of the of the compute Julia sets. No modification is made to the plotting function. The results of the execution time is !!!
execution time (s): 0.107000112534 execution time (s): 0.279000043869 execution time (s): 0.123000144958 execution time (s): 0.197000026703
Well that was fast, I used anaconda python distribution, with the MinGW package within it to compile the code with the accelerate module activated.
Now for the comparison to be fair we need to use a similar acceleration trick, by transforming the matlab code into a mex file. This is done and the comparison of the execution times used by matlab mex function with VS 2012 as compiler is given below
Elapsed time is 0.828125000000000 seconds Elapsed time is 2.140625000000000 seconds Elapsed time is 0.953125000000000 seconds Elapsed time is 1.484375000000000 seconds
So even when loading the mex file Cython is faster than matlab, and considering that I am still novice in both the mex files and python –cython conversions. I am sure there is still a huge room for improvement. But this is pretty impressive work by the python and cython community . I am considering seriously migrating completely to Python.

No comments:
Post a Comment
Your comments are most welcomed