Blasius Equation: Some Explorations Part 2

Solution of Blasius Equation in Matlab

A direct attack on the Blasius equation requires some kind of iteration such as a shooting method, because it is a two-point boundary value problem. Fortunately, there is a reformulation of the problem that avoids an iteration. We begin this reformulation by introducing a new dependent variable :

Where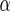 is a positive parameter to be determined. As one may show, the equation for g is then the same as that for f:

From the conditions on f , we have g(0) = 0, and



as

 

Instead of imposing the condition on g at infinity , we impose



Then the problem for g is an initial value problem with initial conditions

In order to carry out this integration numerically using matlab, we need to convert the 3^rd order differential equation into a system of three 1st order equations.

We have the following equivalent system of equations

   1:  >> blas =@(t,f) [f(2); f(3); -0.5*f(1)*f(3)];

   2:  >> options = odeset('RelTol', 1e-10, 'AbsTol', 1e-12);

   3:  >> sol=ode45(blas, [0,15], [0.0 0.0 1.0], options);

   4:  >> plot(sol.x, sol.y(2,:), 'LineWidth', 2.5)

   5:  >> xlabel('\eta'); ylabel('g(\eta)')

   6:  >> plot(sol.x, sol.y(2,:), 'LineWidth', 2.5)

   7:  >> xlabel('\eta'); ylabel('g(\eta)')